Publié le 29 juin 2015 à 20h27 - Dernière mise à jour le 29 septembre 2023 à 8h32
En 1905, un jeune homme de 26 ans, un illustre inconnu mettait au point une théorie scientifique qui allait révolutionner nos concepts d’espace et de temps. Il s’appelait Albert Einstein. Embarquons dans le vaisseau spatio-temporel pour explorer le monde merveilleux de la relativité restreinte et ses quatre dimensions. Auparavant, il faut nous habituer à rejeter nos préjugés les plus tenaces, nos intuitions les plus intimes. Un petit exercice intellectuel va nous aider à jeter un regard sur le monde, un regard libéré des évidences, des apparences.
Mouvement et expériences de pensée
Tout le monde sait (ou croit savoir) ce qu’est le mouvement, tellement il fait partie de notre vie quotidienne. Aristote énonçait une loi partagée par le commun des mortels : le mouvement est lié à une force exercée sur un objet. Dans la vie de tous les jours tout le monde peut en faire l’expérience. Comment mettre en mouvement une bille, qui est dans un état d’immobilité? En la lançant, bien sûr ! Il vous faut pousser une charrette pour la faire avancer, soulever une pierre pour qu’elle suive une trajectoire de bas en haut. Excédé par de tels exemples aussi banals, vous allez m’interrompre et me demander à quoi peuvent bien servir toutes ces analyses. Faut-il vraiment réfléchir intensément pour décrire des exemples aussi quotidiens? Vous me demanderez si, tout compte fait, je ne me moque pas un peu de vous en enfonçant des portes ouvertes. Eh bien, réfléchissons ensemble: voici un chariot. Il est immobile. Vous exercez sur lui une poussée, avec une certaine force. Il va avancer puis s’immobiliser au bout d’un certain temps. Il aura pendant ce laps de temps parcouru une certaine distance. Pourquoi s’immobilise-t-il ? Vous le poussez avec plus de force, de nouveau il va se mettre en mouvement, avec une vitesse supérieure, va parcourir une distance plus grande et s’immobiliser à nouveau. Vous voulez qu’il parcoure une plus grande distance, en exerçant la même force. Vous allez huiler les roues du chariot, enlever toutes les aspérités qui sont sur sa route. Vous le poussez à nouveau avec la même force, et le voilà qu’il parcourt une distance plus grande.
Vous en déduisez que la cause de l’arrêt de la course se situe dans le fait qu’il y a frottement des roues sur la chaussée. Vous en déduisez également que pour qu’il puisse parcourir une distance plus grande, il vous faut éliminer autant que possible le frottement. Remarquez qu’il s’agit dans toutes ces expériences de pousser le chariot avec la même force. Vous faites alors ce que l’on peut appeler une expérience de pensée. Einstein en usait fréquemment. Vous imaginez que vous pouvez éliminer totalement le frottement. Du coup, vous éliminez la cause de l’arrêt du charriot. Vous réalisez alors que ce dernier poursuivra indéfiniment sa course à vitesse constante et en ligne droite. Certes, dans la réalité, vous ne pourrez jamais éliminer totalement le frottement, c’est-à-dire la force qui s’oppose à son mouvement et qui cause son ralentissement puis son immobilité. Mais, par la pensée, vous pouvez faire aisément des expériences impossibles à réaliser concrètement.
Quel est alors le résultat de telles expériences ? D’abord, la force n’est pas responsable du mouvement, car avec la même force, vous pouvez allonger le temps pendant lequel l’objet est en mouvement en éliminant le frottement, qui représente une force opposée à la direction du mouvement du chariot et qui est responsable de son ralentissement et de son arrêt. La force ralentit ou accélère le mouvement. Elle n’est donc pas responsable de la vitesse mais de la modification de la vitesse et de la direction d’un corps. En éliminant totalement le frottement, vous avez permis à l’objet de poursuivre indéfiniment son mouvement, à vitesse constante en ligne droite. Jusqu’à ce qu’une force exercée sur lui ne modifie sa vitesse et sa direction (le frottement constitue une force qui contribue à ralentir le corps). Galilée (1564-1642) avait bien vu qu’aucune force n’était requise pour perpétuer le mouvement rectiligne à vitesse constante, mais c’est Newton qui a formalisé ce principe. Vous pouvez alors énoncer correctement la 1ère loi de Newton, (1643-1727), le principe d’inertie: «Tout corps persévère dans l’état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n’agisse sur lui, et ne le contraigne à changer d’état».
Quels enseignements peut-on tirer d’une telle expérience? D’abord, ne pas se fier à l’évidence. Celle-ci, telle une amie infidèle vous trahira à la première occasion. Ensuite, libéré de l’évidence, ne vous enfermez pas dans les expériences quotidiennes, n’hésitez pas à penser l’expérience, et même si concrètement vous ne pouvez la mener, imaginez la ! A partir d’une expérience de pensée, idéalisée, nous verrons comment Einstein a été amené à découvrir les véritables ressorts de la réalité. Celle-ci ne se dévoile jamais à nu, il faut aller la chercher, et pour cela, il faut penser. Certes, il vous faudra par la suite vérifier vos résultats de pensée en les confrontant à l’expérience et l’expérimentation. Mais n’hésitez pas, à priori, à penser l’improbable, l’inouï. Certes, ne croyez pas qu’il suffise d’un petit effort, il y faut de l’appétit à la connaissance, beaucoup de travail.
Écoutons Einstein qui tire des enseignements de loi de l’inertie dans un livre d’une richesse incroyable, «L’évolution des idées en physique», page 12. Il écrit : «Cette loi ne peut pas être dérivée directement de l’expérience, mais seulement de la pensée spéculative compatible avec l’observation. L’expérience idéalisée ne peut jamais être effectivement réalisée, bien qu’elle conduise à une intelligence profonde des expériences réelles». Avant d’entamer le voyage spatio-temporel, il nous faut dire un mot du principe de relativité de Galilée.
Le principe de relativité galiléen
Voici ce qu’il écrit (Dialogue concernant les deux plus grands systèmes du monde, 1632). «Enfermez-vous avec un ami dans la cabine principale à l’intérieur d’un grand bateau et prenez avec vous des mouches, des papillons, et d’autres petits animaux volants. Prenez une grande cuve d’eau avec un poisson dedans, suspendez une bouteille qui se vide goutte à goutte dans un grand récipient en dessous d’elle. Avec le bateau à l’arrêt, observez soigneusement comment les petits animaux volent à des vitesses égales vers tous les côtés de la cabine. Le poisson nage indifféremment dans toutes les directions, les gouttes tombent dans le récipient en dessous, et si vous lancez quelque chose à votre ami, vous n’avez pas besoin de le lancer plus fort dans une direction que dans une autre, les distances étant égales, et si vous sautez à pieds joints, vous franchissez des distances égales dans toutes les directions. Lorsque vous aurez observé toutes ces choses soigneusement, faites avancer le bateau à l’allure qui vous plaira, pour autant que la vitesse soit uniforme (c’est-à-dire constante) et ne fluctue pas de part et d’autre. Vous ne verrez pas le moindre changement dans aucun des effets mentionnés et même aucun d’eux ne vous permettra de dire si le bateau est en mouvement ou à l’arrêt …» Galilée observe que, dans un navire, aucune expérience de mécanique ne permet de distinguer lorsque le navire est immobile au port de lorsqu’il est en mouvement uniforme.
Autrement dit, et c’est la relativité galiléenne, les lois physiques de la mécanique sont identiques pour tous les référentiels galiléens (en mouvement uniforme c’est-à-dire à vitesse constante en ligne droite). Lâchons le mot : pour Galilée, le mouvement est «comme rien». Du coup, il nous faut revenir sur un terme que nous avons employé : l’immobilité. Si le mouvement n’est comme rien, comment comprendre l’immobilité ? Si vous êtes «immobile» sur le trottoir et que vous observez un véhicule qui circule sur la route, que signifie la phrase: «Le véhicule roule à 90 kilomètres/heure» ?
Ce serait plus exact de dire: «Je suis immobile par rapport au trottoir et le véhicule roule à 90 kilomètres/heure par rapport à moi et au trottoir». Le mouvement est comme rien, cela signifie qu’il est relatif. Un corps est en mouvement par rapport à un autre. Je suis, vous êtes, nous sommes immobiles par rapport à notre planète mais non par rapport à un habitant d’une autre planète qui, lui, s’il le pouvait, nous observerait en mouvement avec la terre.
A bord du vaisseau spatio-temporel
Laissons le monde de l’évidence et posons-nous les bonnes questions. Souvent, ce sont les plus simples qui nous mènent le plus loin.
1905. C’est l’année miraculeuse. Einstein publie dans la revue allemande Annalen der Physik (Annales de la Physique) pas moins de quatre articles qui posent les bases de trois théories fondamentales qui vont bouleverser notre perception du monde : la relativité, la mécanique quantique et le mouvement brownien.
En mars, dans un premier article, il émet l’hypothèse du quantum de lumière, qui ouvre la voie à la mécanique quantique. Pour cette thèse, il obtiendra le prix Nobel.
En mai, dans un deuxième article, il explique le mouvement brownien. Il s’agit d’une description mathématique du mouvement aléatoire d’une «grosse» particule immergée dans un fluide et qui n’est soumise à aucune autre interaction que des chocs avec les «petites» molécules du fluide environnant. Il en résulte un mouvement très irrégulier de la grosse particule, qui a été décrit en 1827 par le botaniste Robert Brown en observant des mouvements de particules à l’intérieur de grains de pollen. Einstein interprète ce mouvement par le choc des molécules du fluide sur les grosses particules, ce qui est un pas fondamental pour prouver l’existence des atomes.
Fin juin, dans un troisième article, il expose sa théorie de la relativité restreinte.
Fin septembre, dans un quatrième article, il traite des conséquences de sa théorie de la relativité restreinte. On y voit notamment apparaître la célèbre formule E=mc2 (équivalence entre la masse et l’énergie).
L’article sur la relativité restreinte est titré : «De l’électrodynamique des corps en mouvement.»
Voici ce qu’Einstein écrit au chapitre sur la simultanéité: «Nous devons prendre en considération le fait que nos conceptions, où le temps joue un rôle, portent toujours sur des évènements simultanés. Par exemple, si nous disons «qu’un train arrive ici à 7 heures», cela signifie «que la petite aiguille de ma montre qui pointe exactement le 7 et que l’arrivée du train sont des événements simultanés. Il peut sembler que toutes les difficultés provenant de la définition du “temps” peuvent être supprimées quand, au “temps”, nous substituons “la position de la petite aiguille de ma montre”». Ce passage est stupéfiant de simplicité. A la grande question philosophique du temps qui a fait couler de l’encre en abondance, Einstein substitue «la position de la petite aiguille de ma montre». Einstein ne cherche pas à en mettre «plein la vue», il décortique un problème en le posant à sa façon, c’est-à-dire en toute simplicité.
Il poursuit: «Une telle définition est dans les faits suffisante, quand il est requis de définir le temps exclusivement à l’endroit où l’horloge se trouve. Mais elle ne suffit plus lorsqu’il s’agit de relier chronologiquement des évènements qui ont lieu à des endroits différents ou ce qui revient au même, d’estimer chronologiquement l’occurrence d’événements qui surviennent à des endroits éloignés de l’horloge.»
En effet, lorsque deux événements surviennent à des endroits éloignés, pour vérifier la simultanéité de ces deux événements (la position de la petite aiguille sur le 7 et l’arrivée du train en gare), il faudra monter tout un système expérimental. Par exemple, un observateur va se placer à mi chemin de la montre et du train. Une personne située dans le train envoie un rayon lumineux lors de l’arrivée du train et celle qui possède la montre en fait de même lorsque sa montre marque 7 heures. Si les rayons lumineux atteignent au même moment la personne placée à mi-chemin, alors on pourra convenir que le train est arrivé à 7 heures. Mais Einstein ne lâche pas le morceau. Et si la personne placée à mi chemin est en mouvement par rapport aux deux autres? Cette fois-ci, plus de dérobade. Il faut bien analyser la question telle qu’elle se pose.
La chevauchée fantastique sur un rayon de lumière
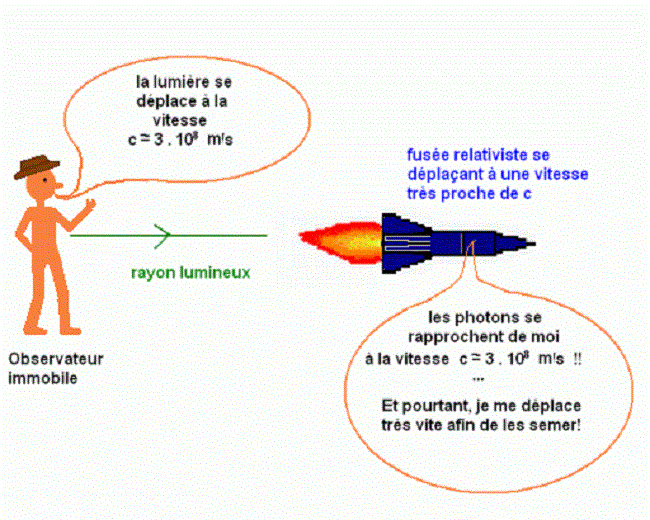
Il nous faut tout d’abord parler de James Clerk Maxwell 1831- 1879). Il est principalement connu pour avoir unifié les phénomènes électriques et magnétiques. Il a notamment démontré que les champs électriques et magnétiques se propagent dans l’espace sous la forme d’une onde et à la vitesse de la lumière. Or, une onde se propage dans un milieu matériel, c’est du moins ce qu’en disait la mécanique classique. Si vous lancez une pierre dans l’eau, vous aller voir se former des ondes portées par le milieu de l’eau. Le son se propage dans l’air. Placez un cloche sous verre dans lequel vous avez préalablement fait le vide, vous n’entendrez pas le son de la cloche. Selon les équations de Maxwell et les différentes expériences pour mesurer la vitesse de la lumière, tout indiquait que cette vitesse est constante, quel que soit le mouvement de la source. En clair, si la lumière vient vers vous ou si elle s’éloigne de vous, vous la verrez toujours se promener à environ 300 000 kilomètres à la seconde. Cela contredisait l’expérience que l’on pouvait faire en faisant rouler une balle dans le wagon d’un train à une vitesse de 60 kilomètres/heure par rapport au train.
Prenons un train en marche et qui roule à 10km/heure par rapport au quai. Si un individu est dans le train, il verra la balle circuler à 60 kilomètres/heure, puisque telle est la vitesse de la balle par rapport au train. Mais, un individu sur le quai verra la balle circuler à 60 km/h (la vitesse de la balle dans le train) + 10 kilomètres/heure (la vitesse du train par rapport au quai) si la balle et le train suivent un mouvement qui pointe dans la même direction. Si les directions de la balle et du train sont opposées, l’observateur sur le quai verra la balle circuler à 60 – 10 km/h, donc à 50Km/h. En revanche, pour tout individu assis dans le train, la vitesse de la balle restera inchangée, c’est à dire 60km/h.
Prenons deux véhicules, l’un de couleur rouge allant à la vitesse de 60Km/h par rapport à la route, l’autre de couleur bleue à 50Km/h. Celui qui est dans le véhicule bleu verra le véhicule rouge le dépasser à 10Km/h. Si les deux véhicules vont à la même vitesse, l’un et l’autre seront réciproquement immobiles.
Et Einstein, à 16 ans, de se demander ce qu’il percevrait s’il chevauchait un rayon de lumière. Il verrait une onde qui ne se déplace pas. Comment concevoir de la lumière immobile. Or, avec les équations de Maxwell, Einstein était rassuré; jamais il ne pourrait voir un tel spectacle : une onde de lumière stationnaire. Toutefois, cette constance de la vitesse de la lumière, on l’a dit, était contraire à la loi de l’addition des vitesses pour deux observateurs en mouvement l’un par rapport à l’autre. Si la lumière est une onde, quel est le milieu qui permet sa propagation ? Les physiciens avaient inventé un milieu matériel grâce auquel la lumière pouvait se propager : l’éther.
Selon notre mouvement par rapport à l’air, le son est plus ou moins rapide, et donc plus grave ou plus aigu. Or, la vitesse de la lumière est constante. Cela signifie qu’elle ne se déplace pas avec l’éther mais à travers l’éther. Un éther immobile et à travers lequel la lumière se déplace.
Un corps immobile ? Selon le principe de relativité, le mouvement à vélocité constante (vitesse et direction conservées) est comme rien, on ne le sent pas. Toutes les lois de la nature sont équivalentes quel que soit le mouvement relatif. D’ailleurs, on ne peut savoir si un bateau est en panne ou s’il est en marche (à vélocité constante). Rappelez-vous les expériences de Galilée dans son bateau. Un éther immobile, cela signifie que tous les observateurs ne sont pas qualifiés de la même façon pour effectuer des expériences. Il y aurait un système préférentiel, celui où l’on est au repos par rapport à l’éther immobile. Cela contredisait le principe de relativité. Comment imaginer que la nature ne présente pas les mêmes lois selon les mouvements qu’effectuent les différents observateurs. Qu’est ce que les lois de la nature ont à voir avec nos mouvements relatifs ? Comment pourrait-elle se déterminer par rapport à nous ? Fini l’objectivité des lois de la nature, fini toute science, tout savoir. Non, cela ne se peut pas pour un Einstein. La nature serait incompréhensible, inabordable. Einstein compris que l’éther posait plus de problème qu’il n’en résolvait et en vint à la seule solution rationnelle : éliminer l’éther. La lumière ne se propage dans aucun milieu mais dans le vide. Il fallait bien tenir les deux bouts de la relativité et de la constance de la vitesse de la lumière, et les ériger en principes intangibles.
Deux principes à la base de la théorie de la relativité restreinte
Oui, le principe de relativité est vrai. Les lois de la nature sont indépendantes des mouvements des observateurs. Tout mouvement est relatif, le repos absolu n’existe pas, tout comme le mouvement absolu. Si l’on effectue une mesure de vitesse, il faut savoir qui mesure et par rapport à qui ou à quoi on mesure.
Oui, le principe de la constance de la vitesse de la lumière est vrai. Ces deux principes se contrarient. Mais au fait, pourquoi en est-il ainsi ?
Reprenons la méthode d’Einstein. Posons les problèmes sans les compliquer à l’extrême. Une vitesse, c’est quoi ? Qu’est ce que je veux signifier dans la phrase : «mon véhicule roule à 90Km/h» (sous entendu, par rapport à la route).
Je veux dire que mon véhicule parcourt une distance de 90 kilomètres en une durée d’une heure. Donc, la vitesse, c’est une distance divisée par une durée. Si j’effectue 90 kilomètres en 2 heures, je divise 90 par 2 (la distance par la durée) et j’en déduis que mon véhicule roule à 45 km/h.
Vous allez me dire ; ça va, on a compris ! Très bien, poursuivons.
Qu’est ce qu’une distance ? C’est la mesure de l’espace qui sépare 2 points.
Qu’est ce qu’une durée ? C’est la mesure de temps compris entre 2 événements. Donc, la vitesse est liée à l’espace et au temps. Vous me voyez venir ? Je poursuis.
Je suis dans un train. Il roule à 10km/h par rapport au quai. Comme je participe au mouvement du train, je suis immobile par rapport au train, tout comme si j’étais sur la voie ferrée en face d’un train à l’arrêt. C’est la même chose, dans un train en marche ou sur la voie ferrée en face d’un train à l’arrêt, je perçois les mêmes phénomènes qui se produisent dans le train. Je suis donc dans le train. Installé dans un wagon. A ma gauche, le mur A, à ma droite le mur B. Le train va dans la direction AB, de gauche à droite. Au milieu du wagon, on place des lanceurs de balle. L’un lance une balle vers le mur A, dans le sens opposé à la direction du train, l’autre lance une autre balle vers le mur B, dans la direction du train. Les deux balles effectuent leur trajet respectif à la même vitesse. Elles sont lancées en même temps.
Pour moi, qui suis dans le train, cela signifie que le train est immobile par rapport à moi. Je vois les deux balles rouler à la même vitesse, 60km/h par exemple et parcourir la même distance, puisque, par définition, les deux balles sont au milieu du wagon et sont donc équidistantes des murs A et B. Deux balles à la même vitesse, parcourant la même distance, il est facile de comprendre que la durée de leur parcours est la même et que les deux balles atteindront leur mur respectif au même moment, donc simultanément. Voilà ce que je perçois en étant un passager du train. Les deux balles atteignent les murs A et B simultanément. Que se passe t-il pour celui qui voit les événements à partir du quai. Le train est en mouvement par rapport à lui.
Il voit la balle qui se dirige vers le mur A parcourir le trajet à une vitesse égale à 60km/h (la vitesse de la balle dans le train) moins 10km/h (la vitesse du train) par rapport au quai. Il faut effectuer une soustraction puisque la balle se dirige à l’opposé de la direction du train. Pour celui qui est sur le quai elle avance vers le mur A à une vitesse du 60Km/h mais recule dans le même temps de 10Km/h. La balle se dirige donc vers le mur A à une vitesse de 50Km/h. Mais, puisque le mur A se déplace dans le sens du train, cela signifie qu’il se rapproche de la balle à une vitesse de 10Km/h. En fait, pour celui qui se situe sur le quai, cette balle va parcourir un moindre trajet mais à une vitesse plus petite. Admettons (c’est une hypothèse farfelue mais qu’importe, le raisonnement reste juste) que le wagon a une longueur de 120 Kilomètres. Donc, chaque balle, au départ se situe à 60Kilomètres de leur mur respectif. La balle dont nous venons d’analyser le mouvement va effectuer dans une heure un trajet de 60Km moins 10Km, car le mur qu’elle veut atteindre se rapproche d’elle à la vitesse de 10 km/h/. En fait, la balle va effectuer un trajet de 50 km à 50 km/h et va donc atteindre le mur A dans l’heure qui suit.
Qu’en est-il pour la balle qui se dirige vers le mur B. Elle va dans le sens du train et donc sa vitesse sera de 60Km/h + 10Km/h, c’est-à-dire 70Km/h.
Mais au fur et à mesure qu’elle se rapproche de son but, le mur B fuit la balle, en tout cas, c’est ce que voit le spectateur sur le quai. Cette balle va donc parcourir dans l’heure 10Kilomètres de plus (la vitesse du train par rapport au quai.). Elle va donc parcourir les 60 kilomètres qui la séparait au départ du mur B + 10 km, donc 70Km.
Résumons. Une balle parcourt une distance de 50 km à une vitesse de 50 km/h. L’autre une distance de 70 km à une vitesse de 70 km/h. Pour celui qui est sur le quai, comme pour celui qui est dans le train, les deux balles atteindront donc leur mur respectif en une heure et les deux événements seront simultanés pour un observateur comme pour l’autre.
Si la vitesse est une distance divisée par une durée, cela signifie que pour trouver la même durée, il faut à la fois transformer les vitesses et les distances. Dans l’exemple ci-dessus, les vitesses n’étaient pas identiques, les distances non plus, mais la durée était la même pour chaque observateur.
Autrement dit, le temps est universel et passe à la même vitesse pour chaque observateur. Le temps est découplé de l’espace, il existe indépendamment de ce dernier. Le temps, c’est à dire, une durée mesurée dans la galaxie d’Andromède, à deux millions et demi d’années lumière reste la même dans la galaxie qui nous habite, la Voie Lactée.
Voilà ce que l’on croyait avant la théorie de la relativité restreints. Car, de telles mesures prises dans l’exemple ci-dessus ne sont pas justes. On a supposé que les distances et les durées, mesurées dans le wagon et sur le quai devaient être identiques. On peut toujours objecter que «cela va de soi». Mais rien à priori ne nous contraint à affirmer une telle chose. Seule la croyance en l’évidence guide nos propos. Certes, les différences que l’on pourrait supputer sont indétectables pour des vitesses insignifiantes par rapport à celle de la lumière. Que signifie 10km/h ; 60km/h par rapport à la vitesse de la lumière, qui est de 300000 kilomètres à la seconde (un milliard de kilomètres à l’heure) ?
Lorsque le temps perd son universalité
Renouvelons l’expérience, mais cette fois-ci, ce ne sont pas des lanceurs de balles qui se placent au milieu du wagon, mais des personnes qui allument une lampe en même temps. Nous allons remplacer notre bon vieux train par un train-lumière, dont la vitesse n’est pas insignifiante par rapport à celle de la lumière. Le problème reste le même. Un rayon lumineux se projette vers le mur A et un autre vers le mur B
Pour un observateur situé dans le train, rien ne change. Il voit deux rayons lumineux cheminer à la même vitesse et parcourir une même distance. Résultat, les deux rayons lumineux atteindront leur mur respectif simultanément.
Mais que se passe t-il pour l’observateur sur le quai ?
Celui-ci voit toujours un mur qui se rapproche d’un des rayons lumineux tandis que l’autre mur s’éloigne du second rayon lumineux. Les deux rayons vont donc parcourir des trajets différents. Jusque là, rien ne change par rapport aux balles.
Mais voilà l’os. Les vitesses des deux rayons lumineux sont identiques. Rappelez vous, la vitesse de la lumière est une constante, que l’on se rapproche ou que l’on s’éloigne d’elle. Donc, si les vitesses sont les mêmes, mais non les distances, alors, les durées ne peuvent plus être les mêmes. Ce qui signifie que l’observateur sur le quai verra d’abord un rayon lumineux atteindre le mur A et ensuite l’autre rayon lumineux atteindre le mur B. Pour celui qui est dans le train, les deux événements sont simultanés, tandis qu’ils ne le sont pas pour l’observateur situé sur le quai.
Vous n’en revenez pas. Ce n’est pas grave. C’est ainsi. Après tout, les phénomènes et les lois de la nature n’ont pas à se préoccuper de vos sentiments.
Remarquez que le concept de causalité n’est pas remis en question. Que l’événement A précède, suive ou soit simultané à l’événement B n’a rien à voir avec la cause. Car, l’événement A n’est pas la cause de l’événement B et réciproquement. La cause réside dans l’allumage de la lampe. Ce qui signifie que cet événement sera toujours premier, quel que soit l’observateur. A une condition, que les vitesses requises ne soient pas supérieures à celle de la lumière. Nous reviendrons sur cette question dans la partie 2, au sujet de la relativité générale.
Et l’espace dans tout ça ?
Écoutons Einstein. Voici ce qu’il écrit dans le livre «L’évolution des idées en physique», pages 174-175: «Comment devons nous faire pour mesurer un bâton quand il est en mouvement en glissant le long de la barre qui représente le Système de Coordonné (SC)? On pourrait procéder de la façon suivante : A un moment donné, deux observateurs prennent simultanément des photos, l’un de l’origine, l’autre de l’extrémité du bâton. Puisque les images sont prises simultanément, nous pouvons composer les marques sur la barre figurant le SC, avec lesquelles l’origine et l’extrémité du bâton en mouvement coïncident. De cette façon, nous déterminons sa longueur. Il n’y a pas de raison de croire que le résultat de telles mesures sera le même que dans le cas d’un bâton au repos. Puisque les photographies devaient être prises simultanément, ce qui, comme nous le savons déjà, est un concept relatif.» En effet, nous avons vu plus haut que deux événements simultanés pour un observateur dans le train-lumière en mouvement ne le sont plus pour une autre observateur situé sur le quai.
Les effets du mouvement sur l’espace
Rejoignons deux frères, Jules et Jim sur un circuit automobiles. Jules a acheté une voiture et a pris soin, chez le concessionnaire, de mesurer la longueur de sa voiture à l’aide d’un mètre. Maintenant que Jules roule à toute allure à bord de son bolide, Jim, resté sur le bord de la piste, ne peut pas vérifier la taille de l’engin par la même méthode. Il procède donc ainsi : Il déclenche son chronomètre dès que le pare-chocs avant arrive à sa hauteur et l’arrête au passage du pare-chocs arrière. Pour calculer la longueur du véhicule, il n’a plus qu’à multiplié le temps ainsi obtenu par sa vitesse.
Jules, dans sa voiture, selon son point de vue est immobile tandis que Jim se déplace, de sorte que le chronomètre de ce dernier lui semble tourner au ralenti. Jules en conclut que la mesure indirecte de Jim sera erronée, qu’elle lui fournira un résultat plus court que celui obtenu à l’arrêt. En effet, dans son calcul, Jim multiplie la vitesse de la voiture par le temps qu’il mesure … à l’aide d’un chronomètre ralenti. La durée mesurée est plus courte qu’elle ne devrait l’être, et la longueur s’en trouve diminuée d’autant. Donc, Jim voit le bolide de Jules plus court en mouvement qu’au repos. C’est un phénomène qui vaut pour tous les objets en déplacement : on les perçoit raccourcis dans la direction de leur trajectoire. On lit parfois dans des livres que le temps passe plus vite ou moins vite selon tel ou tel observateur. Mais que peut donc signifier la vitesse du temps, qui plus est, un temps qui n’est pas universel. Si le temps passe plus ou moins vite, c’est par rapport à quelle vitesse ? A la vitesse «normale» du temps ? Mais comment un temps qui n’est pas universel pourrait-il avoir une vitesse «normale»? Quelle serait cette vitesse? En fait, chacun mesure son temps ici, par exemple sur terre. Pour ce qui concerne le temps pour les habitants de lointaines galaxies, suivons le conseil que César donne à son fils Marius : «Laisse mesurer les autres».
Chacun a son temps qui lui est propre
En vérité, ce que la théorie de la relativité nous explique, c’est que chacun a un temps qui lui est propre. Si j’emporte un livre dans une fusée à grande vitesse, comment me faudra t-il pour lire ce livre sachant qu’il me faut une heure lorsque je suis chez moi ?
Je m’installe dans la fusée, j’emporte mon livre et ma montre qui ne quitte pas mon poignée. Si je commence à lire à 8 heures à ma montre, quelle heure sera-t-il lorsque ma lecture sera terminée. Neuf heures, j’aurais mis 1 heure à ma montre pour le lire, tout comme je mets une heure à ma montre lorsque je le lis bien assis dans mon fauteuil, dans ma maison. Si un observateur extérieur m’observe, il s’apercevra que ma montre retarde, que les aiguilles avancent plus lentement que celles de la sienne.
On appelle ces phénomènes le ralentissement du temps et la contraction de l’espace, mais attention, ne vous y trompez pas, le temps ne ralentit pas, chacun mesure son temps propre qui n’est pas le même pour deux observateurs en mouvement l’un par rapport à l’autre, à des vitesses relativistes (non insignifiantes par rapport à la vitesse de la lumière). Prenons un exemple pour montrer le «ralentissement» du temps. Un simple schéma permettrait de s’en persuader. Confectionnons une montre particulière, appelons la, montre à photon.

L’image du haut représente une montre à photon immobile par rapport à un observateur. Un photon (une particule de lumière) se déplace de bas en haut, puis rebondit et se déplace de haut en bas. La partie du bas est muni d’un détecteur et chaque fois qu’un photon heurte la paroi du bas, un « tic » se fait entendre. Imaginons que l’aller retour dure une seconde pour un observateur, appelons le Henri, immobile par rapport à la montre. Pour lui, le photon parcourt un trajet vertical de bas en haut puis un trajet vertical de haut en bas et un « tic » se fait entendre. 3600 tics correspondent à une durée d’une heure.
Imaginons que soudain, venant de sa gauche, une montre à photon passe à toute allure devant lui, se délaçant de gauche à droite (l’image du bas). Que voit l’observateur ? Le photon ne parcourt plus une trajectoire verticale de bas en haut puis de haut en bas, mais une trajectoire inclinée. En fait, lorsque le photon part du bas, il lui faut un certain temps pour atteindre le haut, et comme la montre se déplace, l’observateur mesure une trajectoire plus longue. Il en est de même lorsque le photon effectue son déplacement de haut en bas.
La distance parcourue par le photon en mouvement est plus longue que celle parcourue par celui qui est immobile par rapport à l’observateur. Et comme le photon garde la même vitesse, cela signifie qu’une durée plus longue est mesurée entre deux «tic» en ce qui concerne le photon en mouvement et donc que les secondes passent plus lentement. Selon l’observateur, la montre en mouvement retardera par rapport à celle qui est immobile. Imaginons que la montre en mouvement se trouve au poignet d’un observateur appelé Hervé. Pour lui, la situation serait réciproque. Il verrait la montre d’Henri retarder par rapport à la sienne. Pour lui, c’est Henri et sa montre qui sont en mouvement alors que lui et sa montre sont immobiles. Remarquez que plus la vitesse à laquelle se meut une montre est importante, plus le trajet est long et donc plus la durée s’allonge entre deux «tic».
L’union de l’espace et du temps
Il nous faut faire un dernier effort. Il nous faut imaginer l’espace-temps.
On a vu que le temps ralentit et l’espace se contracte. Tout se passe comme s’il y avait un jeu de rôles entre les deux. Imaginons un circuit dont le but est de faire des essais de vitesse pour des voitures de courses. Le parcourt se situe du sud au nord. A chaque essai, on pousse les bolides à 200km/h. Premier essai, le parcourt est fait en 1 heure. Deuxième essai, la durée du parcourt est identique. Au troisième essai, la durée est plus longue. Le pilote nous assure qu’il a gardé la même vitesse. Comment expliquer cette différence ?
Après maintes recherches, on s’aperçoit que lors du troisième essai, le soleil se trouvait en face le pilote et l’éblouissait. Il a fallu alors faire un écart vers l’est, de sorte que, la trajectoire suivie déviait de la droite reliant le sud et le nord. Plus la déviation est marquée, et plus la distance parcourue est grande. (Cela ne vous rappelle t-il pas l’exemple de la montre à photon en mouvement par rapport à un observateur et dont la trajectoire était déviée pour celui-ci). Tout se passe comme si le pilote avait partagé sa vitesse en deux parties, dans deux directions différentes : une dont la trajectoire se déplace vers le nord et l’autre dont la trajectoire se déplace vers le nord-est. En partageant sa vitesse dans deux directions, tout se passe comme s’il avait ralenti, puisque le trajet a été plus long. Et voici ce qu’il faut retenir. La vitesse, le mouvement d’un corps s’effectue dans les dimensions de l’espace et du temps. La vitesse se partage entre ses deux dimensions. On ne peut plus penser l’espace et le temps indépendamment l’un de l’autre. Il n’y a pas d’une part un espace tridimensionnel et un temps unidimensionnel, mais un espace temps à quatre dimensions. Eh oui, la quatrième dimension n’a rien de mystérieux, c’est le temps ! Un objet immobile par rapport à nous ne se déplace pas dans les dimensions spatiales et son mouvement ne s’effectue donc que dans une seule dimension, celle du temps. Tout ce qui autour de nous est au repos et vieillit au même rythme, c’est-à-dire progresse dans le temps à la même vitesse. Si un objet se déplace également dans l’espace, sa trajectoire qui était uniquement temporelle est maintenant déviée. Si le mouvement est partagé entre les directions de temps et d’espace, alors sa vitesse temporelle en est diminuée d’autant et l’objet voyage plus lentement dans le temps. En fait, la vitesse spatiale d’un objet ne représente donc que la manière dont son trajet dans le temps est dévié. Si un corps se déplace à la vitesse de la lumière, cela signifie que la totalité de son déplacement s’effectue dans l’espace, il n’a plus aucun déplacement disponible pour se mouvoir dans le temps. Ainsi, un objet qui se déplace à la vitesse de la lumière ne peut plus se déplacer dans le temps, celui-ci est donc figé. En clair, un photon ne vieillit pas. Vous avez remarqué, on ne parle pas de la vitesse du temps, mais de la progression dans le temps d’un corps à une vitesse donnée. Chacun mesure son temps propre selon le mouvement qu’il effectue dans l’espace et le temps.
Et E = MC2 dans tout ça ?
Einstein a montré que l’énergie (E) et la masse (m) d’un objet matériel ne sont pas deux grandeurs indépendantes mais que l’énergie s’obtient à partir de la masse (en la multipliant par le carré de la vitesse de la lumière (C). Donc, à partir d’une petite masse, on obtient une énergie énorme (puisqu’il faut multiplier cette masse par le carré de la vitesse de la lumière, qui représente un chiffre impressionnant).
Ainsi, rien ne peut aller plus vite que la vitesse de la lumière, car, plus un objet est massif, plus il est difficile de l’accélérer. La masse d’une particule augmente au fur et à mesure que sa vitesse approche celle de la lumière. Pour qu’il atteigne la vitesse C il faudrait lui fournir une énergie infinie, ce qui est évidemment impossible.
Conclusion : rien ne peut se déplacer plus vite que la vitesse de la lumière, donc aucune information n’est instantanée, aucune force n’exerce une action instantanée sur un corps. Or, la force de gravité de Newton se transmettait instantanément d’une masse à l’autre. Si on enlevait le soleil, pour Newton, l’effet s’en ferait instantanément ressentir sur terre. Pour Einstein, c’est impossible. Ainsi, la première contradiction rencontrée par la physique classique avait trait au principe de relativité qui était incompatible avec la constance de la vitesse de la lumière. Einstein devait résoudre cette contradiction en élaborant la théorie de la relativité restreinte.
Or, une autre contradiction pointait son nez, l’impossibilité de transmettre quelque action que ce soit instantanément. Cela heurtait la théorie de la gravitation universelle élaborée par Newton. Albert Einstein, de nouveau devait la résoudre en élaborant, dix ans plus tard, en 1915, la théorie de la relativité générale. Celle-ci est à la base de notre compréhension de l’Univers. C’est cette théorie que nous allons examiner dans une prochaine rubrique.
Lectures conseillées concernant les trois rubriques déjà en ligne :
-«Le boson et le chapeau mexicain», Gilles Cohen Tannoudji et Michel Spiro, Éditions Gallimard, 2013
-«La mélodie secrète», Trinh Xuan Thuan, Editions Gallimard, 1991, pour la préface
-«Origines», Trinh Xuan Thuan, Editions Gallimard, Librairie Arthème Fayard, 2003
-«La relativité», Albert Einstein, Editions Gauthier-Villars 1956, repris dans la Petite Bibliothèque Payot en 1963
-«L’évolution des idées en physique», Albert Einstein et Léopold Infeld, Éditions Flammarion, 1983
-« L’univers élégant », Brian Greene, Éditions Robert Laffont, 2000




